Cara Menyelesaikan Pertidaksamaan Pecahan, Akar, Nilai Mutlak, Polinomial, Contoh Soal & Pembahasan

Daftar Materi Matematika

• 1. Logaritma: Sifat, Operasi Hitung dan Penerapan
• 2. Fungsi atau Pemetaan
• 3. Sistem Persamaan Linear Dua Variabel
• 4. Sistem Persamaan Linear Tiga Variabel
• 5. Logika Matematika

Advertisement

Baca Juga:

Pertidaksamaan dalam matematika adalah kalimat atau pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih. Beberapa notasi dasar dalam pertidaksamaan adalah sebagai berikut.

Tabel Notasi Pertidaksamaan Matematika

Notasi	Arti	Contoh
<	Lebih kecil Kurang dari	2 < 3 x + 1 < 3
>	Lebih besar Lebih dari	3 > 2 3x + 1 > 5
≤	Lebih kecil atau sama dengan Maksimum/maksimal Sebanyaknya Paling banyak Tidak lebih dari Sekurangnya	2 ≤ 3 x + 1 ≤ 3
≥	Lebih besar atau sama dengan Minimum/minimal Sesedikitnya Paling sedikit Tidak kurang dari selebihnya	3 ≥ 2 3x + 1 ≥ 5
≠	Tidak sama dengan	2 ≠ 3
a < x < b	Diantara a dan b	2 < x < 5
a ≤ x < b	Diantara a dan b bila nilai minimal a	2 ≤ x < 5
a < x ≤ b	Diantara a dan b bila maksimal b	2 < x ≤ 5
a ≤ x ≤ b	Diantara a dan b bila minimal a dan maksimal b	2 ≤ x ≤ 5

Jenis-jenis pertidaksamaan dalam matematika ada banyak sekali, di antaranya pertidaksamaan linear, kuadrat, akar, pecahan, nilai mutlak dan polinomial. Nah pada kesempatan kali ini kita akan membahas cara menentukan himpunan penyelesaian dari beberapa jenis pertidaksamaan matematika tersebut.

1. Menentukan Penyelesaian Pertidaksamaan Pecahan

Secara umum, penyelesaian atau himpunan penyelesaian pertidaksamaan berbentuk pecahan berikut ini.

f(x)	<	0
g(x)

f(x)	≤	0
g(x)

f(x)	>	0
g(x)

f(x)	≥	0
g(x)

Dapat ditentukan melalui langkah-langkah sebagai berikut.

Langkah 1:

Carilah nilai-nilai nol bagian pembilang dan bagian penyebut dari bentuk pecahan f(x)/g(x), yaitu f(x) = 0 dan g(x) = 0.

Langkah 2:

Gambarlah nilai-nilai nol itu pada diagram garis bilangan, sehingga diperoleh interval-interval.

Langkah 3:

Tentukan tanda-tanda interval dengan cara mensubtitusikan nilai-nilai uji yang berada dalam masing-masing interval.

Langkah 4:

Berdasarkan tanda-tanda interval yang diperoleh pada langkah 3, kita dapat menentukan interval yang memenuhi. Dalam menentukan interval yang memenuhi itu, perlu diingat adanya syarat bahwa bagian penyebut tidak boleh sama dengan nol atau g(x) ≠ 0.

Sekarang agar kalian lebih paham mengenai cara menentukan himpunan penyelesaian dari pertidaksamaan bentuk pecahan, silahkan kalian pelajari dan pahami dua contoh soal dan pembahasannya berikut ini.

Contoh Soal :

Carilah himpunan penyelesaian dari pertidaksamaan pecahan berikut ini.

2x – 4	≤	0
3x + 3

Jawab:

Nilai nol bagian pembilang: 2x – 4 = 0 ⇒ x = 2

Nilai nol bagian penyebut: 3x + 3 = 0 ⇒ x = −1

Nilai nol pembilang dan penyebut ditempatkan pada diagram garis bilangan. Nilai-nilai nol tersebut membagi garis bilangan menjadi tiga interval yaitu x < −1, −1 < x < 2, dan x > 2. Perhatikan gambar berikut ini.

Kemudian kita tentukan tanda interval cukup dengan menggunakan satu nilai uji. Ambil angka yang paling mudah dihitung, yaitu x = 0 yang terlatak dalam selang −1 < x < 2. Apabila nilai x = 0 kita masukkan ke pertidaksamaan pecahan, maka kita peroleh:

2(0) – 4	=	−	4
3(0) + 3			3

Karena hasilnya negatif, maka interval −1 < x < 2 bertanda −  atau < 0.

Karena satu interval sudah diketahui, maka dua interval lainnya juga dapat dengan mudah ditentukan, yaitu interval x < −1 bertanda positif dan interval x > 2 juga bertanda positif, karena setiap melompati pembuat nol, tanda harus berganti (selang-seling) seperti yang diperlihatkan pada gambar berikut.

Dengan mengingat bahwa bagian penyebut tidak boleh sama dengan nol, maka:

⇔ 3x + 3 ≠ 0

⇔ 3x ≠ 3

⇔ x ≠ 3/3

⇔ x ≠ 1

Sehingga tanda selang pada gambar garis bilangan di atas berubah menjadi seperti berikut.

Jadi, himpunan penyelesaian dari pertidaksamaan tersebut adalah HP = {x | −1 < x ≤ 2}.

2. Menentukan Penyelesaian Pertidaksamaan Bentuk Akar

Pertidaksamaan bentuk akar sering disebut juga pertidaksamaan irrasional, yaitu pertidaksamaan yang variabelnya terdapat dalam tanda akar. Pertidaksamaan bentuk akar mempunyai 8 macam bentuk baku (umum) yaitu sebagai berikut.

1.	√u(x) < a		1.	√u(x) < √v(x)
2.	√u(x) ≤ a		2.	√u(x) ≤ √v(x)
3.	√u(x) > a		3.	√u(x) > √v(x)
4.	√u(x) ≥ a		4.	√u(x) ≥ √v(x)

Dengan a ≥ 0, a ∈ R (a bilangan real positif atau nol).

u(x) dan v(x) merupakan fungsi-fungsi dalam x dengan u(x) ≥ 0 dan v(x) ≥ 0.

Misalkan kita memiliki dua bilangan p dan q.

■ Misalkan p = 5 maka 52 = 25

q = 8 maka 82 = 64

Tampak bahwa 0 < 5 < 8 dan 52 < 82

■ Misalkan p = 1 maka 12 = 1

q = 3 maka 32 = 9

Tampak bahwa 0 < 1 < 3 dan 12 < 32

Berdasarkan contoh di atas, secara umum dapat dikatakan sebagai berikut.

Jika p dan q ∈ R dengan 0 < p < q,

maka p2 < q2

Dengan sifat tersebut, kita dapat menyelesaikan sistem pertidaksamaan bentuk akar dengan langkah-langkah sebagai berikut.

1. Kuadratkan kedua ruas pertidaksamaan itu (tanda pertidaksamaan tetap). Kemudian, selesaikan.

2. Tentukan syarat bahwa bentuk akar masing-masing ruas terdefinisi atau bernilai real, yaitu bilangan di bawah tanda akar bernilai positif atau nol.

3. Tentukan interval yang memenuhi penyelesaian pada langkah pertama dan langkah kedua (cari irisannya).

Agar kalian lebih memahami cara penyelesaian pertidaksamaan bentuk akar, perhatikan beberapa contoh soal dan pembahasannya berikut ini.

Contoh Soal :

Carilah himpunan penyelesaian pertidaksamaan irasional berikut.

√x + 5 < 4

Jawab:

1. Kedua ruas dikuadratkan, sehingga diperoleh pertidaksamaan berikut.

⇒ (√x + 5)2 < 42

⇒ x + 5 < 16

⇒ x < 16 – 5

⇒ x < 11 ……………. (1)

2. Syarat u(x) ≥ 0

⇒ x + 5 ≥ 0

⇒ x ≥ −5 …………… (2)

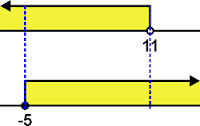
3. Penyelesaian yang memenuhi dari (1) dan (2) adalah irisan kedua interval itu. Jadi, penyelesaiannya adalah −5 ≤ x < 11. Dengan demikian, himpunan penyelesaiannya adalah {x | −5 ≤ x < 11, x ∈ R}. Himpunan penyelesaian ini tampak pada garis bilangan di bawah ini.

3. Menentukan Penyelesaian Pertidaksamaan Nilai Mutlak

Nilai mutlak dari suatu bilangan real x (dilambangkan dengan |x|) adalah nilai tak negatif dari bilangan rea itu. Misalnya, |3| = 3, |−2| = 2, dan |−1/2| = 1/2. Nilai mutlak bilangan nol didefinisikan sebagai bilangan itu sendiri, sehingga | 0 | = 0. Secara umum, nilai mutlak didefinisikan sebagai berikut.

Untuk setiap bilangan real x, nilai mutlak x, ditulis |x| diartikan

|x|	=	x, untuk x ≥ 0
		−x, untuk x < 0

Misalkan |x| < 0 maka dapat ditentukan suatu bilangan positif p sehingga |x| + p = a, a ≥ 0. Oleh karena itu,

|x| + p = a

⇔ (|x| + p)2 = a2

⇔ x2 + 2p|x| + p2 = a2

Karena p positif dan |x| positif, jika dimisalkan q = 2p|x| + p2 maka q merupakan bilangan positif, sehingga diperoleh bahwa x2 + q = a2. Karena x2 + q (positif) = a2 maka dapat disimpulkan bahwa

|x|

<

a, untuk a ≥ 0 ⇔ x2 < a2

Analogi dengan cara di atas maka kita juga akan memperoleh

|x|

>

a, untuk a ≥ 0 ⇔ x2 > a2

Cobalah kalian buktikan.

Akibat dari sifat |x| < a, untuk a ≥ 0 ⇔ x2 < a2 adalah sebagai berikut.

x2 < a2

⇔ x2 – a2 < 0

⇔ (x – a)(x + a) < 0

Pembuat nol di ruas kiri pertidaksamaan itu adalah

(x – a)(x + a) < 0

⇔ x – a = 0 atau x + a = 0

⇔ x = a atau x = −a

Gambar garis bilangannya adalah sebagai berikut.

Kemudian kita uji sebuah titik, misalnya 0 (nol).

(x – a)(x + a) = 0

x = 0 → (0 – a)(0 + a)

⇔ (−a)(a)

⇔ −(a)2 < 0

Karena untuk x = 0 bernilai negatif (−a2 < 0) maka pernyataan tersebut benar sehingga tanda dari garis bilangan itu adalah sebagai berikut.

Interval yang memenuhi pertidaksamaan itu adalah –a < x < a.

Akibat dari sifat |x| > a, untuk a ≥ 0 ⇔ x2 > a2 adalah sebagai berikut.

x2 > a2

⇔ x2 – a2 > 0

⇔ (x – a)(x + a) > 0

Pembuat nol ruas kiri pertidaksamaan itu adalah x = a a tau x = −a dan garis bilangannya adalah sebagai berikut.

Karena daerah yang diminta positif, maka daerah yang memenuhi adalah x < −a atau x > a seperti yang diperlihatkan pada gambar berikut.

Analog dengan kedua hal di atas, tentu kalian dapat menunjukkan bahwa |x| ≤ a, a ≥ 0 ⇔ −a ≤ x ≤ a dan untuk |x| ≥ a, a ≥ 0 ⇔ x ≤ −a atau x ≥a. Jadi, dapat disimpulkan bahwa untuk a ≥ 0, berlaku

|x| < a ⇔ −a < x < a

|x| ≤ a ⇔ −a ≤ x ≤ a

|x| > a ⇔ x < −a atau x > a

|x| ≥ a ⇔ x ≤ −a atau x ≥ a

Pertidaksamaan nilai mutlak adalah suatu pertidaksamaan yang variabelnya berada dalam tanda mutlak. Misalnya,

|x – 1| < 3, |x2 + 3x| > |5 – 2x|, dan |x + 1|2 – 2 ≤ |x + 1|.

Dari uraian di atas, untuk menyelesaikan suatu pertidaksamaan nilai mutlak, dapat kita gunakan sifat-sifat berikut.

Jika a ∈ R dan a ≥ 0 maka
1.	a.	|x| < a ⇔ −a < x < a
	b.	|x| ≤ a ⇔ −a ≤ x ≤ a
	c.	|x| > a ⇔ x < −a atau x > a
	d.	|x| ≥ a ⇔ x ≤ −a atau x ≥ a
2.	|x| = √x2

Contoh Soal:

Tentukanlah himpunan penyelesaian pertidaksamaan berikut.

|2x – 3| ≤ 7

Jawab:

Dengan menggunakan sifat 1 (b), diperoleh:

−7 ≤ 2x – 3 ≤ 7

⇔ −7 + 3 ≤ 2x ≤ 7 + 3

⇔ −4 ≤ 2x ≤ 10

⇔ −2 ≤ x ≤ 5

Jadi, himpunan penyelesaiannya adalah {x| −2 ≤ x ≤ 5, x ∈ R}.

4. Menentukan Penyelesaian Pertidaksamaan Polinomial

Bentuk polinomial adalah bentuk suku banyak. Dalam bentuk khusus, polinomial berderajat dua biasa disebut bentuk kuadrat. Bentuk umum polinomial adalah sebagai berikut.

anxn + an – 1xn – 1 + an – 2xn – 2 + … + a1x + a0

Pertidaksamaan yang akan kita bahas kali ini lebih ditekankan pada pertidaksamaan polinomial yang dapat difaktorkan. Bagaimana cara menyelesaikannya? Ikuti langkah-langkah berikut ini.

1. Faktorkan suku banyak itu.

2. Tentukan pembuat nol suku banyak.

3. Gambar garis bilangan yang memuat pembuat nol.

4. Tentukan interval di mana bernilai positif dan di mana bernilai negatif. Tanda daerah terdekat (setelah melewati pembuat nol) berubah tanda jika pangkat ganjil, sedangkan jika pangkatnya genap, tanda tidak berubah.

Misalkan:

(x – a)3(x – b)(x – c) ≥ 0

(x – a)2(x – b)(x – c) ≥ 0

5. Tentukan daerah yang memenuhi persoalan tersebut.

Contoh Soal :

Tentukan penyelesaian dari pertidaksamaan x2(x – 2)(x + 3) < 0.

Jawab:

x2(x – 2)(x + 3) < 0

pembuat nolnya adalah sebagai berikut.

● x2 = 0 ⇔ x = 0

● x – 2 = 0 ⇔ x = 2

● x + 3 = 0 ⇔ x = −3

Gambar garis bilangan yang memuat tiga pembuat nol tersebut adalah sebagai berikut.

Kemudian kita tentukan tanda interval, dengan memasukkan salah satu nilai x.

Misalkan untuk x = 1 maka:

⇒ x2(x – 2)(x + 3)

⇒ (1)2(1 – 2)(1 + 3)

⇒ (1)(−1)(4)

⇒ −4

Karena −4 < 0, maka tanda interval yang memuat nilai x = 1 bernilai negatif. Kita ketahui bahwa variabel x berpangkat 2 (genap), itu artinya sebalah kanan dan kiri nilai pembuat nol untuk x2 (dalam hal ini 0) harus bertanda sama, yaitu negatif.

Dengan demikian dua tanda interval yang tersisa yaitu di sebelah kiri -3 dan sebelah kanan 2 harus bertanda positif. Tanda-tanda interval pada garis bilangan di atas adalah sebagai berikut.

Karena yang diminta dalam soal adalah himpunan bilangan yang lebih kecil atau sama dengan nol (< 0), maka penyelesaiannya adalah daerah negatif. Berikut ini gambar garis bilangan penyelesaian pertidaksamaan yang diminta.

Jadi, himpunan penyelesaiannya adalah HP = {x| −3 < x  < 0 atau 0 < x < 2, x ∈ R}.