Hubungan Konjungsi 2 Pernyataan & Gabungan 2 Himpunan, Contoh Soal dan Pembahasan
https://blogmipa-matematika.blogspot.com/2018/03/hubungan-konjungsi-dan-gabungan-himpunan.html
Daftar Materi Matematika
Advertisement
Baca Juga:
Konjugsi adalah pernyataan yang dibentuk dari dua pernyataan p dan q yang dirangkai dengan menggunakan kata hubung “dan” yang disimbolkan dengan “∧”. Untuk menentukan nilai tabel kebenaran dari konjungsi, perhatikan contoh berikut ini.
Misalkan:
p: Tahun 2008 adalah tahun kabisat.
q: Tahun 2008 memiliki 29 hari pada bulan Februari.
sekarang, kita tentukan negasi dari p dan q yaitu sebagai berikut.
~p: Tahun 2008 bukan tahun kabisat.
~q: Tahun 2008 tidak memiliki 29 hari pada bulan Februari.
Dari pernyataan di atas, kita dapat membuat hubungan konjungsi sebagai berikut.
1. Tahun 2008 adalah tahun kabisat dan memiliki 29 hari pada bulan Februari.
(kalimat tersebut bernilai benar)
2. Tahun 2008 adalah bukan tahun kabisat dan memiliki 29 hari pada bulan Februari.
(kalimat tersebut bernilai salah karena tidak mungkin ada bulan Februari berjumlah 29 hari, sedangkan tahunnya tidak kabisat).
3. Tahun 2008 adalah tahun kabisat dan tidak memiliki 29 hari pada bulan Februari.
(kalimat tersebut salah karena setiap tahun kabisat pasti jumlah hari bulan Februari adalah 29).
4. Tahun 2008 bukan tahun kabisat dan tidak memiliki 29 hari pada bulan Februari.
(kalimat tersebut salah karena jelas bahwa tahun 2008 merupakan tahun kabisat dan jumlah hari pada bulan Februari adalah 29.)
Dari deskripsi di atas, dapat kita susun tabel nilai kebenaran dari konjungsi, yaitu sebagai berikut.
Tabel Nilai Kebenaran Konjungsi
p
|
q
|
p ∧ q
|
B
|
B
|
B
|
B
|
S
|
S
|
S
|
B
|
S
|
S
|
S
|
S
|
Contoh Soal 1:
Diberikan dua pernyataan berikut ini.
p: Mangga adalah nama buah (benar)
q: Mangga adalah buah berbentuk balok (salah)
Tentukan kalimat konjungsi dan nilai kebenarannya.
Jawab:
p ∧ q: Mangga adalah nama buah dan berbentuk balok, bernilai salah.
Contoh Soal 2:
Carilah nilai x agar setiap kalimat berikut ini menjadi konjungsi yang benar.
a) 2x – 3 = 5 dan √40 = 2√10
b) 1 – 3x = 2x – 4 dan log 2 + log 3 = log 6
c) 2x = 16 dan 2log 16 = 4
Jawab:
a) Terdapat sebuah kalimat terbuka yaitu p(x): 2x – 3 = 5 dan pernyataan q: √40 = 2√10. Nilai kebenaran pernyataan q kita tentukan sebagai berikut.
⇒ √40 = √4 × √10
⇒ √40 = 2 × √10
⇒ √40 = 2√10
Dengan demikian, pernyataan q bernilai benar (B). Agar p ∧ q menjadi konjungsi yang benar maka kalimat terbuka p(x) harus bernilai benar sehingga nilai x yang memenuhi adalah sebagai berikut.
⇒ 2x – 3 = 5
⇒ 2x = 5 + 3
⇒ 2x = 8
⇒ x = 8/2
⇒ x = 4
Jadi, agar 2x – 3 = 5 dan √40 = 2√10 menjadi konjungsi yang benar, maka nilai x adalah 4.
b) Terdapat sebuah kalimat terbuka yaitu p(x): 1 – 3x = 2x – 4 dan pernyataan q: log 2 + log 3 = log 6. Nilai kebenaran pernyataan q kita tentukan sebagai berikut.
⇒ log 2 + log 3 = log (2 × 3)
⇒ log 2 + log 3 = log 6
Dengan demikian, pernyataan q bernilai benar (B). Agar p ∧ q menjadi konjungsi yang benar maka kalimat terbuka p(x) harus bernilai benar sehingga nilai x yang memenuhi adalah sebagai berikut.
⇒ 1 – 3x = 2x – 4
⇒ 2x + 3x = 1 + 4
⇒ 5x = 5
⇒ x = 5/5
⇒ x = 1
Jadi, agar 1 – 3x = 2x – 4 dan log 2 + log 3 = log 6 menjadi konjungsi yang benar, maka nilai x adalah 1.
c) Terdapat sebuah kalimat terbuka yaitu p(x): 2x = 16 dan pernyataan q: 2log 16 = 4. Nilai kebenaran pernyataan q kita tentukan sebagai berikut.
⇒ 2log 16 = 2log 24 = 4
Dengan demikian, pernyataan q bernilai benar (B). Agar p ∧ q menjadi konjungsi yang benar maka kalimat terbuka p(x) harus bernilai benar sehingga nilai x yang memenuhi adalah sebagai berikut.
⇒ 2x = 16
Jadi, agar 1 – 3x = 2x – 4 dan log 2 + log 3 = log 6 menjadi konjungsi yang benar, maka nilai x adalah 1.
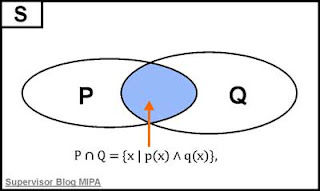
Hubungan antara Konjungsi Dua Pernyataan dengan Irisan Dua Himpunan
Jika P dan Q masing-masing merupakan himpunan penyelesaian dari kalimat terbuka p(x) dan q(x) pada himpunan semesta S, maka P ∩ Q adalah himpunan penyelesaian dari kalimat terbuka p(x) ∧ q(x) pada himpunan semesta S yang sama.
|
Dalam bentuk lambang himpunan dapat dituliskan sebagai berikut.
P = {x | p(x)}, p benar jika x ∈ P}
Q = {x | q(x)}, Q benar jika x ∈ Q}
P ∩ Q = {x | p(x) ∧ q(x)}, p ∧ q benar jika x ∈ (P ∩ Q)}
Hubungan tersebut dapat digambarkan dengan diagram Venn seperti yang ditunjukkan pada gambar di bawah ini.
Contoh Soal 3:
Diketahui p(x): x2 – 5x + 4 = 0 dan q(x): 3 ≤ x ≤ 5 dengan x peubah pada himpunan bilangan asli A. Pernyataan p dan q dibentuk dari p(x) dan q(x) dengan mengganti nilai x ∈ A. Carilah nilai x sehingga (p ∧ q) bernilai benar.
Jawab:
Himpunan penyelesaian p(x): x2 – 5x + 4 = 0 adalah P = {1, 4}
Himpunan penyelesaian q(x): 3 ≤ x ≤ 5 adalah Q = {3, 4, 5}
Irisan P dan Q adalah P ∩ Q = {4}
(p ∧ q) benar, jika x ∈ P ∩ Q, berarti nilai x = 4.