Pertidaksamaan Pecahan: Bentuk Umum, Sifat, Metode Penyelesaian, Contoh Soal dan Pembahasan
https://blogmipa-matematika.blogspot.com/2018/01/pertidaksamaan-pecahan.html
Daftar Materi Matematika
Advertisement
Baca Juga:
Bentuk Umum Pertidaksamaan Pecahan
Perhatikan pertidaksamaan-pertidaksamaan berikut ini.
(a)
|
1
|
>
|
0
|
x
|
(b)
|
x – 1
|
<
|
0
|
x + 2
|
(c)
|
x2 – 6
|
≥
|
0
|
x2 – 6x + 3
|
(d)
|
x3 – 8
|
≤
|
0
|
x2 – 4x
|
Pertidaksamaan-pertidaksamaan di atas dinamakan pertidaksamaan pecahan. Pertidaksamaan pecahan memiliki empat macam bentuk umum atau bentuk baku yakni sebagai berikut.
1.
|
f(x)
|
<
|
0
|
g(x)
|
2.
|
f(x)
|
≤
|
0
|
g(x)
|
3.
|
f(x)
|
>
|
0
|
g(x)
|
4.
|
f(x)
|
≥
|
0
|
g(x)
|
Dengan f(x) dan g(x) merupakan fungsi-fungsi dalam x, dan g(x) ≠ 0.
Sifat-Sifat Pertidaksamaan Pecahan
Perhatikan bentuk pecahan 1/4. Pecahan 1/4 > 0 karena 1 > 0 dan 4 > 0. Namun, coba perhatikan bentuk −1/−4. Bentuk −1/−4 = 1/4 > 0. Ternyata, jika −1 < 0 dan −4 < 0 akan berakibat −1/−4 = 1/4 > 0. Jadi, dapat dikatakan bahwa:
a/b > 0 ⇔ a > 0 dan b > 0 atau a < 0 dan b < 0
|
Hal ini diperluas untuk suatu fungsi misalkan f(x) dan g(x).
f(x)/g(x) > 0 ⇔ f(x) > 0 dan g(x) > 0 atau f(x) < 0 dan g(x) < 0
|
Sekarang cobalah untuk bentuk pecahan −1/4. Karena −1 < 0 dan 4 > 0 maka −1/4 < 0. Jadi, pada pertidaksamaan f(x)/g(x) < 0 akan berlaku.
f(x)/g(x) < 0 ⇔ f(x) < 0 dan g(x) > 0 atau f(x) > 0 dan g(x) < 0
|
Lebih lanjut, berlaku pula untuk pertidaksamaan f(x)/g(x) ≥ 0 dan f(x)/g(x) ≤ 0, yaitu sebagai berikut.
●
|
f(x)/g(x) ≥ 0 ⇔ f(x) ≥ 0 dan g(x) > 0 atau f(x) ≤ 0 dan g(x) < 0
|
●
|
f(x)/g(x) ≤ 0 ⇔ f(x) ≥ 0 dan g(x) < 0 atau f(x) ≤ 0 dan g(x) > 0
|
Dengan sifat-sifat di atas, kalian dapat menyelesaikan pertidaksamaan pecahan. Perhatikan beberapa contoh soal dan pembahasannya berikut ini.
Contoh Soal 1:
Carilah penyelesaian dari pertidaksamaan berikut ini.
a.
|
x – 2
|
>
|
0
|
x + 3
|
b.
|
3x – 2
|
≤
|
0
|
x + 1
|
Jawab:
a. Kita gunakan sifat di atas yaitu sebagai berikut.
x – 2
|
>
|
0
|
x + 3
|
⇒ x – 2 > 0 dan x + 3 > 0 atau x – 2 < 0 atau x + 3 < 0.
Dalam hal ini, f(x) = x – 2 dan g(x) = x + 3.
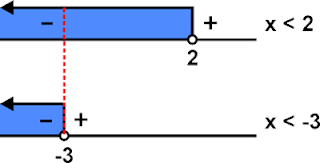
● Untuk x – 2 > 0 dan x + 3 > 0 berarti x > 2 dan x > −3. Selanjutnya, kita buat garis bilangan berikut daerah arsiran yang merupakan penyelesaian dari kedua pertidaksamaan. Garis bilangan dan daerah arsirannya tampak pada gambar berikut ini.
Setelah itu, kita tentukan irisan daerah arsiran dari kedua garis bilangan berarsir itu, yaitu sebagai berikut.
Dari gambar tersebut, tampak bahwa irisan daerah arsiran (daerah yang sama-sama terkena arsiran) adalah x > 2.
● Untuk x – 2 < 0 dan x + 3 < 0, berarti x < 2 dan x < −3.
Jika digambarkan dalam garis bilangan tampak sebagai berikut.
Dari gambar irisan tersebut tampak bahwa penyelesaian untuk x – 2 < 0 dan x + 3 < 0 adalah x < −3.
Dengan demikian, penyelesaian dari pertidaksamaan berikut ini
x – 2
|
>
|
0
|
x + 3
|
adalah {x | x > 2 atau x < −3}.
b. Untuk pertidaksamaan pecahan yang kedua berlaku sifat sebagai berikut.
3x – 2
|
≤
|
0
|
x + 1
|
⇒ 3x – 2 ≥ 0 dan x + 1 < 0 atau 3x – 2 ≤ 0 dan x + 1 > 0.
● Untuk 3x – 2 ≥ 0 dan x + 1 < 0 , berarti x ≥ 2/3 dan x < −1.
Daerah penyelesaiannya dapat digambarkan dalam garis bilangan berikut ini.
Dari gambar tersebut, terlihat bahwa tidak ada daerah dari kedua garis bilangan itu yang beririsan sehingga dapat disimpulkan bahwa tidak ada nilai x yang memenuhi pertidaksamaan:
3x – 2
|
≤
|
0
|
x + 1
|
● Untuk 3x – 2 ≤ 0 dan x + 1 > 0, berarti x ≤ 2/3 dan x > −1.
Jika digambarkan dalam garis bilangan tampak seperti gambar di bawah ini.
Berdasarkan gambar di atas, terlihat bahwa daerah −1 < x ≤ 2/3 merupakan daerah yang sama-sama terkena arsiran (beririsan).
Jadi, berdasarkan dua kemungkinan di atas, penyelesaian dari pertidaksamaan pecahan berikut ini
3x – 2
|
≤
|
0
|
x + 1
|
adalah {x | −1 < x ≤ 2/3}.
Metode Penyelesaian Pertidaksamaan Pecahan
Metode untuk menyelesaikan pertidaksamaan pecahan menggunakan garis bilangan, dapat juga dilakukan dengan langkah-langkah berikut.
■ Tentukan pembuat nol bagian pembilang dan penyebut dari pecahan itu, yaitu f(x) = 0 dan g(x) = 0.
■ Lukislah nilai-nilai pembuat nol itu pada garis bilangan sehingga diperoleh interval-interval.
■ Lukislah tanda-tanda (+ atau −) pada interval dengan mensubtitusikan nilai-nilai yang berada dalam masing-masing interval.
■ Tentukan interval yang memenuhi pertidaksamaan tersebut. (Ingat: bagian penyebut tidak boleh sama dengan nol atau g(x) ≠ 0).
Dengan metode tersebut, kalian akan lebih cepat menentukan himpunan penyelesaian pertidaksamaan pecahan yang diberikan. Sekarang coba kalian pahami contoh soal berikut ini.
Contoh Soal 1:
Carilah himpunan penyelesaian dari pertidaksamaan pecahan berikut ini.
a.
|
3x – 6
|
≤
|
0
|
2x + 4
|
b.
|
x2 – 2x – 3
|
>
|
0
|
x2 – 4
|
c.
|
x + 4
|
≤
|
1
|
x + 1
|
2
|
Jawab:
a. Pertidaksamaan ini dapat diselesaikan dengan langkah-langkah sebagai berikut.
■ Nilai-nilai pembuat nol
Bagian pembilang: 3x – 6 = 0 ⇔ x = 2
Bagian penyebut: 2x + 4 = 0 ⇔ x = −2
■ Garis bilangan dari pembuat nol itu tampak seperti pada gambar di bawah ini.
■ Misalkan dipilih x = 0. Dengan mensubtitusikan x = 0 ke ruas kiri pertidaksamaan maka diperoleh:
3x – 6
|
=
|
3(0) – 6
|
=
|
−
|
6
|
<
|
0
|
2x + 4
|
2(0) + 4
|
4
|
Karena hasilnya lebih kecil daripada nol (0), maka interval pada x = 0 bertanda negatif.
Jika satu interval sudah diketahui tandanya, maka dua interval lain dapat dengan mudah ditentukan tandanya tanpa menguji nilai dalam interval tersebut. Caranya adalah dengan menggunakan teknik selang-seling yaitu dua tanda yang berdampingan selalu berlawanan, misal: sebelah kiri negatif, maka sebelah kanan positif dan seterusnya. Dengan cara tersebut, maka tanda pada interval pembuat nol tersebut adalah sebagai berikut.
■ Bagian penyebut tidak sama dengan nol, g(x) ≠ 0 sehingga x = −2 bukan termasuk daerah penyelesaian. Oleh karena itu, himpunan penyelesaiannya adalah {x | −2 < x ≤ 2, x ∈ R}. Penyelesaian ini tampak pada garis bilangan berikut.
b. Pertidaksamaan pecahan ini dapat dikerjakan dengan langkah yang sama seperti di atas, yaitu sebagai berikut.
Pembuat nol bagian pembilang:
x2 – 2x – 3 = 0
⇒ (x – 3)(x + 1) = 0
⇒ x = 3 dan x = −1
Pembuat nol bagian penyebut:
x2 – 4 = 0
⇒ (x – 2)(x + 2) = 0
⇒ x = 2 dan x = −2
Karena x2 – 4 ≠ 0, maka tentu saja x ≠ 2 atau x ≠ −2
Jika digambarkan dalam garis bilangan, tampak sebagai berikut.
Untuk menentukan tanda (+ atau −), pilih titik x = 0 untuk pengujian dengan cara mensubtitusikan ke pertidaksamaan pecahannya.
x2 – 2x – 3
|
=
|
02 – 2(0) – 3
|
=
|
3
|
>
|
0
|
x2 – 4
|
02 – 4
|
4
|
Karena hasilnya sama lebih besar dari nol (0), maka interval yang memuat x = 0 bertanda negatif. Dengan menggunakan teknik selang-seling, maka tanda pada 3 interval lainnya adalah sebagai berikut.
Karena yang diminta adalah lebih besar dari nol (> 0), maka himpunan penyelesaiannya adalah interval yang bertanda positif (+) seperti yang diperlihatkan pada daerah arsiran dalam gambar garis bilangan berikut ini.
Jadi, himpunan penyelesaiannya adalahn {x | x < −2, −1 < x < 2, atau x > 3}.
c. Langkah pertama adalah memindahkan suku di ruas kanan ke ruas kiri sehingga diperoleh:
x + 4
|
≤
|
1
|
x + 1
|
2
|
⇒
|
x + 4
|
−
|
1
|
≤
|
0
|
x + 1
|
2
|
⇒
|
2(x + 4) − (x + 1)
|
≤
|
0
|
2(x + 1)
|
⇒
|
x + 7
|
≤
|
0
|
2x + 2
|
Pembuat nol bagian pembilang adalah x = −7. Syarat lain bagian penyebut tidak sama dengan nol maka 2x + 2 ≠ 0 ⇔ x ≠ −1. Dengan cara yang sama diperoleh garis bilangan berikut ini.
Karena yang diminta adalah kurang dari atau sama dengan nol (≤ 0), maka himpunan penyelesaiannya adalah {x | −7 ≤ x < −1}.