Cara Menentukan Penyelesaian SPLK Berbentuk Eksplisit

Daftar Materi Matematika

• 1. Logaritma: Sifat, Operasi Hitung dan Penerapan
• 2. Fungsi atau Pemetaan
• 3. Sistem Persamaan Linear Dua Variabel
• 4. Sistem Persamaan Linear Tiga Variabel
• 5. Logika Matematika

Advertisement

Baca Juga:

Sistem persamaan linear dan kuadrat atau disingkat SPLK adalah sistem persamaan yang terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yang masing-masing bervariabel dua. Berdasarkan karakteristik dan bagian bentuk kuadratnya, sistem persamaan linear dan kuadrat (SPLK) dapat dibedakan menjadi dua jenis, yaitu SPLK dengan bagian kuadrat berbentuk eksplisit dan SPLK dengan bagian kuadrat berbentuk implisit.

Nah, pada kesempatan kali ini kita akan belajar mengenai cara menentukan himpunan penyelesaian dari SPLK dengan bagian kuadratnya berbentuk eksplisit. Secara umum, bentuk baku dari SPLK dengan bagian kuadrat berbentuk eksplisit dapat ditulis sebagai berikut.

y = ax + b	……………. (bagian linear)
y = px2 + qx + r	……………. (bagian kuadrat)

Dengan a, b, p, q, dan r merupakan bilangan-bilangan real.

Untuk memahami cara menentukan penyelesaian atau himpunan penyelesaian sistem persamaan linier dan kuadrat, simaklah SPLK berikut ini.

y = x + 2 ………. bagian linear

y = x2 …………… bagian kuadrat

Subtitusikan bagian linier y = x + 2 ke bagian kuadrat y = x2, sehingga kita peroleh:

⇒ x + 2 = x2

⇒ x2 – x – 2 = 0

Kita peroleh persamaan kuadrat dalam x. Dengan cara pemfaktoran, kita peroleh nilai x sebagai berikut.

⇒ x2 – x – 2 = 0

⇒ (x + 1)(x – 2) = 0

⇒ x = −1 atau x = 2

Kemudian subtitusikan x = −1 atau x = 2 ke persamaan y = x + 2 atau y = x2 sehingga kita peroleh:

⇒ y = −1 + 2

⇒ y = 1

dan

⇒ y = 2 + 2

⇒ y = 4

atau

⇒ y = (−1)2

⇒ y = 1

dan

⇒ y = (2)2

⇒ y = 4

Jadi, himpunan penyelesaian SPLK tersebut adalah {(−1, 1), (2, 4)}.

Secara geometri, anggota-anggota dari himpunan penyelesaian SPLK di atas dapat ditafsirkan sebagai koordinat titik potong antara garis y = x + 2 dengan parabola y = x2. Coba kalian perhatikan gambar di bawah ini.

Secara umum, penyelesaian atau himpunan penyelesaian dari SPLK

y = ax + b

y = px2 + qx + r

dapat ditentukan melalui langkah-langkah sebagai berikut.

Langkah pertama:

Subtitusikan bagian linear y = ax + b ke bagian kuadrat y = px2 + qx + r, sehingga diperoleh:

⇒ ax + b = px2 + qx + r

⇒  px2 + qx – ax + r – b = 0

⇒  px2 + x(q – a) + (r – b) = 0, merupakan persamaan kuadrat dalam x.

Langkah kedua:

Nilai-nilai x pada langkah pertama (jika ada) disubtitusikan ke persamaan y = ax + b atau y = px2 + qx + r. Namun untuk efisiensi waktu, cukup subtitusikan ke persamaan linearnya saja.

Kita ingat bahwa nilai x yang memenuhi persamaan kuadrat px2 + x(q – a) + (r – b) = 0 disebut akar-akar dari persamaan kuadrat itu. Banyaknya nilai x (banyak akar) dari persamaan kuadrat tersebut ditentukan oleh nilai diskriminan D = (q – a)2 – 4p(r – b). Dengan demikian, banyak anggota dalam himpunan penyelesaian SPLK

y = ax + b

y = px2 + qx + r

ditentukan oleh nilai diskriminan D = (q – a)2 – 4p(r – b) sebagai berikut.

■ Jika D > 0, maka SPLK mempunyai dua anggota dalam himpunan penyelesaiannya.

■ Jika D = 0, maka SPLK tepat mempunyai satu anggota dalam himpunan penyelesaiannya.

■ Jika D < 0, maka SPLK tidak mempunyai anggota dalam himpunan penyelesaiannya. Dikatakan himpunan penyelesaiannya adalah himpunan kosong dan ditulis ∅.

Anggota-anggota dari himpuna penyelesaian SPLK dapat ditafsirkan secara geometri sebagai koordinat titik potong antara garis y = ax + b dengan parabola y = px2 + qx + r. Kedudukan garis terhadap parabola itu ditentukan oleh nilai diskriminan D = (q – a)2 – 4p(r – b) sebagai berikut.

■ Jika D > 0, maka garis memotong parabola di dua titik yang berlainan.

■ Jika D = 0, maka garis memotong parabola tepat di sebuah titik. Dalam hal demikian, dikatakan garis menyinggung parabola.

■ Jika D < 0, maka garis tidak memotong maupun menyinggung parabola.

Pada gambar berikut ini diperlihatkan tiga kemungkinan kedudukan garis y = ax + b terhadap parabola y = px2 + qx + r.

Contoh Soal

Carilah himpunan penyelesaian dari tiap sistem persamaan linear dan kuadrat (SPLK) berikut ini, kemudian buatlah grafik penyelesaiannya (sketsa tafsiran geometri).

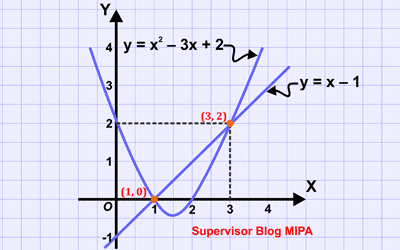
a. y = x – 1 dan y = x2 – 3x + 2

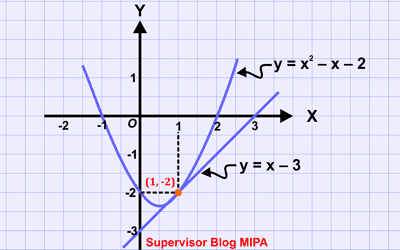
b. y = x – 3 dan y = x2 – x – 2

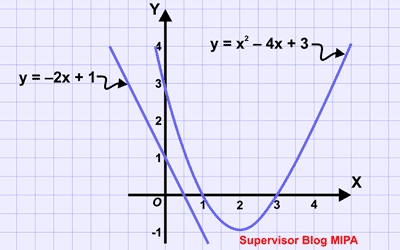
c. y = −2x + 1 dan y = x2 – 4x + 3

Jawab:

a. Subtitusikan bagian linear y = x – 1 ke bagian kuadrat y = x2 – 3x + 2, sehingga diperoleh:

⇒ x – 1 = x2 – 3x + 2

⇒ x2 – 3x – x + 2 + 1 = 0

⇒ x2 – 4x + 3 = 0

⇒ (x – 1)(x – 3) = 0

⇒ x = 1 atau x = 3

Nilai x = 1 atau x = 3 disubtitusikan ke persamaan y = x – 1.

Untuk x = 1 diperoleh y = 1 – 1 = 0 → (1, 0)

Untuk x = 3 diperoleh y = 3 – 1 = 2 → (3, 2)

Jadi, himpunan penyelesaiannya adalah {(1,0), (3,2)}. Tafsiran geometrinya, garis y = x – 1 memotong parabola y = x2 – 3x + 2 di dua titik yang berlainan yaitu di (1, 0) dan di (3, 2). Perhatikan gambar di bawah ini.

b. Subtitusikan y = x – 3 ke y = x2 – x – 2 sehingga diperoleh:

⇒ x – 3 = x2 – x – 2

⇒ x2 – x – x – 2 + 3 = 0

⇒ x2 – 2x + 1 = 0

⇒ (x – 1)2 = 0

⇒ x = 1

Nilai x = 1 disubtitusikan ke persamaan y = x – 3 sehingga didapatkan

⇒ y = 1 – 3 = −2 → (1, −2)

Jadi, himpunan penyelesaiannya adalah {(1, −2)}. Tafsiran geometrinya, garis y = x – 3 menyinggung parabola y = x2 – x – 2 di titik (1, −2). Perhatikan gambar di bawah ini.

c. Subtitusikan y = −2x + 1 ke  y = x2 – 4x + 3, diperoleh

⇒ −2x + 1 = x2 – 4x + 3

⇒ x2 – 4x + 2x + 3 – 1 = 0

⇒ x2 – 2x + 2 = 0

Persamaan kuadrat ini tidak mempunyai akar real, karena D = (−2)2 – 4(1)(2) = −4 < 0. Jadi, himpunan penyelesaiannya adalah himpunan kosong, ditulis ∅. Tafsiran geometrinya, garis y = −2x + 1 tidak memotong maupun menyinggung parabola y = x2 – 4x + 3. Perhatikan gambar berikut.

Demikianlah artikel tentang cara mudah menentukan himpunan penyelesaian SPLK dengan menggunakan grafik tafsiran geometri. Semoga dapat bermanfaat untuk Anda.