Cara Merasionalkan Penyebut Pecahan Bentuk Akar Beserta Contoh Soal dan Pembahasannya
https://blogmipa-matematika.blogspot.com/2017/05/merasionalkan-pecahan-bentuk-akar.html
Daftar Materi Matematika
Advertisement
Baca Juga:
Dalam artikel tentang pengertian, rumus, dan operasi hitung bentuk akar telah dijelaskan bahwa bentuk akar adalah akar dari bilangan rasional yang hasilnya adalah bilangan irasional. Contohnya adalah √3, √5, √6, √7 dan sebagainya. Nah pada artikel ini akan membahas tentang cara merasionalkan penyebut pecahan bentuk akar.
Apa itu Pecahan Bentuk Akar?
Yang dimaksud pecahan bentuk akar adalah bilangan pecahan berbentuk a/√b atau √a/b atau √a/√b dengan a, b ∈ R dan a, b ≠ 0.
Apa Artinya Merasionalkan?
Kata merasionalkan berasal dari kata rasioanal. Sesuai dengan namanya merasionalkan berarti membuat atau mengubah suatu bentuk bilangan yang irasional menjadi bentuk bilangan yang rasional.
Mengapa Penyebut Pecahan Bentuk Akar Harus Dirasionalkan?
Sebenarnya dalam matematika tidak ada keharusan untuk merasionalkan penyebut pecahan bentuk akar. Akan tetapi jika penyebut suatu pecahan berbentuk bilangan irasional seperti misalkan 2/√3 itu sama artinya dengan 2/1.7320508075688772935274463415059… Sehingga penulisan bilangan penyebut akan terlalu panjang . Jika kita gambarkan bentuk pecahannya akan seperti ini:
Terlalu panjang bukan gambar garis pembaginya?
Namun jika penyebut pecahan 2/√3 dirasionalkan menjadi 2/3 √3 maka gambar bentuk pecahannya akan menjadi seperti ini:
Garis pembagi pembilang dengan penyebut tidak terlalu panjang meskipun hasil dari √3 sangat panjang tetapi setidaknya bentuk yang ke-2 ini lebih sederhana dari bentuk yang pertama. Jadi dapat disimpulkan bahwa fungsi merasionalkan penyebut pada pecahan bentuk akar adalah untuk membuat pecahan bentuk akar menjadi lebih sederhana.
Bagaimana Cara Merasionalkan Penyebut Pecahan Bentuk Akar?
Pada pengertian pecahan bentuk akar di atas, pecahan bentuk akar ada yang berbentuk a/√b atau √a/b atau √a/√b. Namun sebenarnya bentuk pecahan masih banyak lagi selain ketiga bentuk tersebut. Dan masing-masing bentuk memiliki cara perasioanalan yang berbeda-beda. Untuk memahami cara merasionalkan pecahan bentuk akar, simak baik-baik penjelasan berikut ini.
Cara Merasionalkan Pecahan Berbentuk a/√b
Cara merasionalkan bentuk a/√b adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk sekawan dari penyebutnya yaitu √b. Rumusnya adalah sebagai berikut:
Contoh:
Rasionalkanlah bentuk pecahan di bawah ini!
7/√2
Jawab:
=(7/√2) x (√2/√2)
= (7 x √2)/(√2 x √2)
= (7√2)/2
= (7/2)√2
Contoh Soal Merasionalkan Pecahan Bentuk a/√b dan Pembahasan
Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah!
- 8/√2
Jawab:
= (8/√2) x (√2/√2)
= (8 x √2)/(√2 x √2)
= (8√2)/2
= 4√2
- 15/√5
Jawab:
= (15/√5) x (√5/√5)
= (15√5)/(√5 x √5)
= (15√5)/5
= 3√5
- 24/√3
Jawab
= (24/√3) x (√3/√3)
= (24√5)/(√3 x √3)
= (24√3)/3
= 8√3
- 12/√6
Jawab
= (12/√6) x (√6/√6)
= (12√6)/(√6 x √6)
= (12√6)/6
= 2√6
Cara Merasionalkan Pecahan Berbentuk c/(a + √b)
Cara merasionalkan bentuk c/(a + √b) adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan lawan dari penyebutnya yaitu (a - √b). Rumusnya adalah sebagai berikut:
Contoh:
Rasionalkanlah bentuk pecahan di bawah ini!
2/(1 + √3)
Jawab:
=[2/(1 + √3)] x [(1 - √3)/(1 - √3)]
=[2 x (1 - √3)] / [(1 + √3) x (1 - √3)]
= (2 – 2 √3)/(1 – 3)
= (2 – 2 √3)/(-2)
= √3 - 1
Contoh Soal Merasionalkan Pecahan Bentuk c/(a + √b) dan Pembahasan
Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah!
- 4/(2 + √2)
Jawab:
= [4/(2 + √2)] x [(2 – √2)/(2 – √2)]
= [4 x (2 – √2)]/[2 + √2) x (2 – √2)]
= (8 – 4 √2)/(4 – 2)
= (8 – 4 √2)/2
= 4 – 2 √2
= 2 (2 - √2)
- 4/(2 + √5)
Jawab:
= [4/(2 + √5)] x [(2 – √5)/(2 – √5)]
= [4 x (2 – √5)]/[2 + √5) x (2 – √5)]
= (8 – 4 √5)/(4 – 5)
= (8 – 4 √5)/(-1)
= 4 √5 – 8
= 4 (√5 – 2)
Cara Merasionalkan Pecahan Berbentuk c/(a - √b)
Cara merasionalkan bentuk c/(a - √b) adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan lawan dari penyebutnya yaitu (a + √b). Rumusnya adalah sebagai berikut:
Contoh:
Rasionalkanlah bentuk pecahan di bawah ini!
8/(1 - √3)
Jawab:
=[8/(1 - √3)] x [(1 + √3)/(1 + √3)]
=[8 x (1 + √3)] / [(1 - √3) x (1 + √3)]
= (8 + 8 √3)/(1 – 3)
= (8 – 8 √3)/(-2)
= 4 √3 – 4
= 4 (√3 – 1)
Contoh Soal Merasionalkan Pecahan Bentuk c/(a - √b) dan Pembahasan
Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah!
- 2/(2 - √3)
Jawab:
= [2/(2 - √3)] x [(2 + √3)/(2 + √3)]
= [2 x (2 + √3)]/[2 - √3) x (2 + √3)]
= (4 + 2 √3)/(4 – 3)
= (4 + 2 √3)/1
= 4 + 2 √3
= 2 (2 + √3)
- 4/(3 - √5)
Jawab:
= [4/(3 - √5)] x [(3 + √5)/(3 + √5)]
= [4 x (3 + √5)]/[3 - √5) x (3 + √5)]
= (12+ 4 √5)/(9 – 5)
= (12 + 4 √5)/4
= 3 + √5
Cara Merasionalkan Pecahan Berbentuk c/(√a + √b)
Cara merasionalkan bentuk c/(√a + √b) adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan lawan dari penyebutnya yaitu (√a - √b). Rumusnya adalah sebagai berikut:
Contoh Soal Merasionalkan Pecahan Bentuk c/(√a + √b) dan Pembahasan
Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah!
- 2/(√3 + √2)
Jawab:
= [2/(√3 + √2)] x [(√3 – √2)/(√3 – √2)]
= [2 x (√3 – √2)]/[(√3 + √2) x (√3 – √2)]
= (2 √3 – 2 √2)/(3 – 2)
= (2 √3 – 2 √2)/1
= 2 √3 – 2 √2
= 2 (√3 – √2)
- 4/(√5 + √3)
Jawab:
= [4/(√5 + √3)] x [(√5 – √3)/(√5 – √3)]
= [4 x (√5 – √3)]/[(√5 + √3) x (√5 – √3)]
= (4 √5 – 4 √3)/(5 – 3)
= (4 √5 – 4 √3)/2
= 2 √5 – 2 √3
= 2 (√5 – √3)
Cara Merasionalkan Pecahan Berbentuk c/(√a - √b)
Cara merasionalkan bentuk c/(√a - √b) adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan lawan dari penyebutnya yaitu (√a + √b). Rumusnya adalah sebagai berikut:
Contoh Soal Merasionalkan Pecahan Bentuk c/(√a - √b) dan Pembahasan
Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah!
- 3/(√6 – √5)
Jawab:
= [3/(√6 – √5)] x [(√6 + √5)/(√6 + √5)]
= [3 x (√6 + √5)]/[(√6 – √5) x (√6 + √5)]
= (3 √6 + 3 √5)/(6 – 5)
= (3 √6 + 3 √5)/1
= 3 √6 + 3 √5
= 3 (√6 + √5)
- 4/(√11 – √7)
Jawab:
= [4/(√11 – √7)] x [(√11 + √7)/(√11 + √7)]
= [4 x (√11 + √7)]/[(√11 – √7) x (√11 + √7)]
= (4 √11 + 4 √7)/(11 – 7)
= (4 √11 + 4 √7)/4
= √11 + √7
Demikianlah artikel tentang cara merasionalkan penyebut pecahan bentuk akar dilengkapi dengan contoh soal dan pembahasannya. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya,
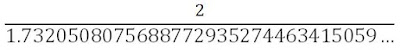





terima kasih atas artikelnya
ReplyDeleteini sangat membantu.😊
semagat terus untuk ilmunya...
kakak adalah seseorang yang peduli denga pelajar.
saya sendiri mewakili sebagai pelajar sangat2 berterima kasih.
😊😊😊
sama-sama...
Deletetangkiyu....sangat bermanfaat...
ReplyDeleteHbnnjnn
ReplyDeleteThank you somuch
ReplyDeleteKurang lengkap artikel nya
ReplyDeleteTks atas pencerahannya
ReplyDelete